(2) 过盈配合

　　保证具有过盈(包括最小过盈等于零)的配合，称过盈配合。 　
　　从孔、轴公差带相对位置看，孔的公差带在轴的公差带以下，就形成过盈配合，如图6-2所示。

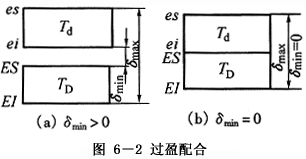
　　从孔、轴的极限尺寸或极限偏差的关系看，当D_max≤d_min或ES≤ei时,形成过盈配合。
　　
　　表示过盈配合要求的松紧程度的特征值是最大极限过盈和最小极限过盈。有时，也用平均过盈表示,平均过盈δav是最大极限过盈和最小极限过盈的平均值，即：
　　　　　　　　　δ_av=(δ_max+δ_min)/2

　　过盈的允许变动量称为过盈公差T_δ，过盈公差等于最大极限过盈与最小极限过盈之差， 即： T_δ=δ_max –δ_min

　　若将极限过盈与孔、轴极限尺寸或极限偏差的关系代入上式，则可得： T_δ=T_d+T_D

　　上式表明，过盈公差等于相互结合的孔、轴尺寸公差之和，过盈公差是表示过盈配合要求的松紧均匀程度即配合精度的特征值。

　　间隙公差和过盈公差统称为配合公差，它们都是结合松紧的允许变动量。