第3节 尺寸链关系
2 精度关系
尺寸链封闭环的精度是由各组成环的精度决定的。依据不同的实际情况,可以采用两种法来计算确定封闭环精度与各组成环精度之间的数值关系:一种是完全互换法,又称极限法;另外一种是大数互换法,又称为概率法。
测量尺寸链各环之间的精度关系是其测量精度关系,是各环的测量误差(测量不确定度)之间的关系,只可以使用概率法进行计算。在使用尺寸链概率法计算时,可以将各环的测量误差(测量不确定度)的极限值类似尺寸精度的上、下偏差进行处理。
1) 完全互换法(极限法)
完全互换法求解尺寸链的基本出发点是只要所有组成环的实际尺寸满足各自精度的要求,则封闭环的实际尺寸一定满足其精度要求。
当所有增环均为最大极限尺寸,且所有减环均为最小极限尺寸时,获得封闭环的最大极限尺寸;当所有增环均为最小极限尺寸,且所有减环均最大极限尺寸时,获得封闭环的最小极限尺寸。
极限尺寸关系为:

极限偏差关系为:

公差关系为:
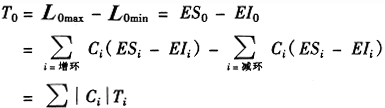
以上关系式中,T0、ES0、EI0、L0max、L0min分别为封闭环的公差、上偏差、下偏差、最大极限尺寸和最小极限尺寸;Ti、ESi、EIi、Limax、Limin分别为第i个组成环的公差、上偏差、下偏差、最大极限尺寸和最小极限尺寸。
对于平面线性尺寸链,Ci=±1,因此T0=∑Ti。即封闭环的公差T0等于各组成环公差之和。由此可见,在尺寸链各环中,封闭环的公差最大,精度最低。