2) 大数互换法（概率法）
　　完全互换法求解尺寸链是按各环的极限尺寸进行计算的。当封闭环与各组成环公差都比较宽松时，容易保证产品的功能要求。当封闭环精度较高，且组成环数较多时，用完全互换法求解尺寸链，将增加组成环的加工难度。实际上，零件在批量生产过程中，其尺寸出现极值的情况非常少。一般情况下，零件的实际尺寸大部分出现在尺寸公差带中心附近，且服从某种统计分布规律。大数互换法基于这种尺寸统计规律进行尺寸链计算。

　　大数互换法求解尺寸链是把各个组成环看作是相互无关的独立随机变量，因此由它们形成的封闭环也是随机变量。通常以相似生产条件得到的统计资料确定实际尺寸在其公差带内分布的信息(即分布规律)。在不改变规定的技术要求的条件下，可以放宽组成环的公差，从而获得更佳的技术经济效益，保证绝大多数封闭环满足设计要求。
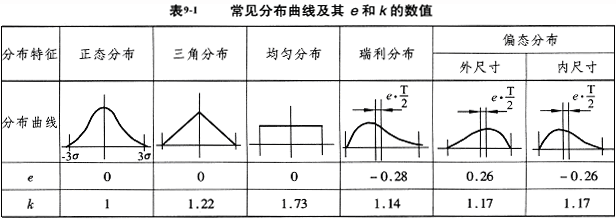
　　组成环常见的几种分布规律如表9-1，表中列出了不同分布规律的相对不对称系数e和相对分布系数k。

　　设各组成环符合的某种分布规律，其相对分布系数和相对不对称系数分别为k_i和e_i, 公差值为T_i。则尺寸链中各环的公差关系为：

　　尺寸链各环公差带的分布中心关系为： μ_i=(ES_i+EI_i)/2
　

　　则封闭环的上、下偏差为
　

　　大批量生产时，可以认为各组成环的实际尺寸均服从正态分布，其e=0、k=1，并以99.73%的置信水平确定其分布范围。封闭环的实际尺寸按随机变量合成，也符合正态分布规律。此时上述计算方法可以简化为以下常用方法。
　　封闭环的标准差σ₀与各组成环标准差σ_i的关系为：
　
　　尺寸链中各环的公差关系为：
　　
　　尺寸链各环公差带的正态分布中心为：
　　
　　则封闭环的上、下偏差为