根据已知若干环的基本尺寸、极限偏差和公差，计算确定其他各环的基本尺寸、极限偏差和公差，称为求解尺寸链，也称为尺寸链计算。
　　若已知所有组成环的基本尺寸、极限偏差和公差，求解封闭环的基本尺寸、极限偏差和公差，称为尺寸链的校核计算。它主要用于验算设计的正确性。
　　若已知封闭环的基本尺寸、极限偏差和公差，求解各组成环的极限偏差和公差，称为尺寸链的设计计算。它主要用于在设计中确定零件各有关尺寸的极限偏差和公差。
　　若已知封闭环和若干组成环的基本尺寸、极限偏差和公差，求解其余各组成环的极限偏差和公差，称为尺寸链的中间计算。中间计算多用于基准换算、工序尺寸计算等。

1 校核计算
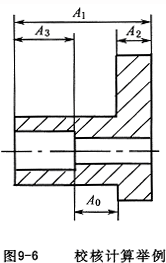
[例9-1] 如图9-6所示零件，图样标注尺寸为
，试求解尺寸A₀。

解：
　　本例中的设计图样上只标注尺寸A₁、A₂和A₃, 没有直接标注尺寸A₀，但A₀是需要保证的间接尺寸，应根据A₁、A₂、A₃来校核A₀的精度，故A₀为封闭环。
　　该零件的尺寸链由A₀、A₁、A₂、A₃四个尺寸组成，是平面线性尺寸链，比较简单，无需单独画出尺寸链图。其尺寸的基本尺寸关系表达式为：A₀=A₁-A₂-A₃
　　很明显，C₁=1、C₂= -1、C₃= -1，A₁为增环，A₂、A₃为减环。封闭环基本尺寸为： A₀=A₁-A₂-A₃=50-10-15=25mm