(1) 直线度误差的最小区域判别准则
　　在给定平面内，由两平行直线包容实际被测要素时，形成高低相间、至少三点接触，即为最小包容区域，如图11—66所示，称为“相间准则”。

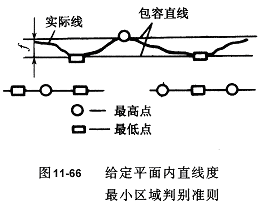
(2) 平面度误差的最小区域判别准则
　　由两平行平面包容实际被测要素时，形成至少四点或三点接触，且具有下列形式之一者，即为最小包容区域： 一个最高(低)点在另一包容平面上的投影位于三个最低(高)点所形成的三角形内称为“三角形准则”(图11-67(a))。 两个最高点的连线与两个最低点的连线在包容平面上的投影相交称为“交叉准则”(图11-67 (b))。 一个最高(低)点在另一包容平面上的投影位于两个最低(高)点的连线上称为“直线准则”(图11-67 (c))。

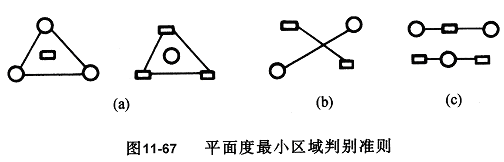
(3) 圆度误差的最小区域判别准则
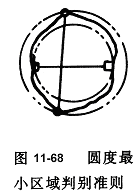
　　由两同心圆包容实际被测要素时，形成内外相间至少四点接触，即为最小包容区域，亦称“相间准则”或“交叉准则”(图11—68)。

2）近似评定方法
　　在实际工作中，除了按形状误差值的定义由最小包容区域的宽度或直径评定形状误差值以外，还可以采用其他近似的评定方法。
(1) 直线度误差的近似评定
　　直线度误差除了按最小包容区域方法评定其误差值以外，对于在给定平面内的直线度误差，还可以用两端点连线法或最小二乘法来评定。
　　用两端点连线法评定给定平面内的直线度误差时，根据测量结果作出实际被测要素的误差图形以后，按其两端点连线的方向作两平行直线包容误差图形，且具有最小距离，则此两平行包容直线沿纵坐标方向的距离即为直线度误差值。
　　用最小二乘法评定给定平面内的直线度误差时，应先确定实际被测要素误差图形的最小二乘线，再作两平行于最小二乘线的直线包容误差图形、且具有最小距离，则此两平行包容直线沿纵坐标方向的距离即为直线度误差值。
　　[例11—2] 设用平直仪测量某导轨的直线度，按图11-69(a)所示依次测得各点读数a_i分别为-0.02、+0.01、-0.03、-0.03、+0.03、+0.01、-0.03、-0.02mm，试分别按两端点连线法、最小二乘法和最小包容区域法评定其直线度误差值。
　　解：
　　平直仪是以仪器光直线为基准，测量后一点相对于前一点的高度差，所以应先将各测点的读数换算到同一坐标系。为此，可取定被测导轨的起始点(第0点)为原点，即其纵坐标值z0=0，则其余各点的坐标值可按z_i=z_i-1+a_i进行累积后得到，如表11—3所列。

表11—3直线度误差的评定

　　按各测点的坐标值zi及相应的点序x_i作出误差图形，如图11—69(b)所示。

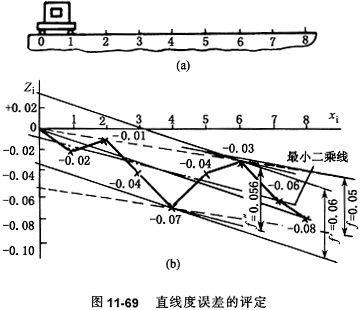
　　由图可见，按两端点连线法评定的直线度误差值为：
　　f'=0.06 mm。
　　若按最小二乘法评定，则最小二乘线的截距a和斜率q分别为a=-0.007、q=-0.008，如图11—69(b)中点划线所示。
　　第4点对最小二乘线的距离：
　　d_min =Z4-(-0.007-0.008x4)=-0.07-(-0.007-0.008X4)=-0.031 mm
　　第6点对最小二乘线的距离：
　　d_max =Z6-(-0.007-0.008x6)=-0.03-(-0.007-0.008X6)=+0.025 mm
　　则按最小二乘法评定的直线度误差值为：
　　f"=d_max-d_min=(+0.025)-(-0.031)=0.056 mm
　　若按最小包容区域法评定，则直线度误差值为： f=0.05 mm。

　　显然，在一般情况下，两端点连线法和最小二乘法的评定结果大于最小包容区域法。当误差图形位于其两端点连线的一侧时，两端点连线法与最小包容区域的评定结果是相同的。