(2) 平面度误差的近似评定
　　除了按最小包容区域的方法以符合三角形准则、交叉准则或直线准则的两平行包容平面间的宽度作为平面度误差值以外，还可以用三远点平面法、对角线平面法和最小二乘法来评定平面度误差，如图11-70。

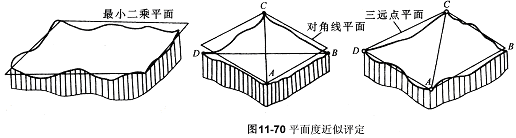
　　用三远点平面法评定平面度误差时，以通过实际被测表面上相距较远的三点的平面作为评定基面，并以实际被测表面对此评定基面的最大变动作为平面度误差值。
　　用对角线平面法评定平面度误差时，以通过实际被测表面上一条对角线的两个对角点、且平行于另一条对角线的平面作为评定基面，并以实际被测表面对此评定基面的最大变动作为平面度误差值。
　　用最小二乘法评定平面度误差时，以实际被测表面的最小二乘平面作为评定基面，并以实际被测表面对此评定基面的最大变动作为平面度误差值。最小二乘平面是使实际被测表面上各点对该平面的距离的平方和为最小的平面。
　　以上四种评定方法都需要将实际被测表面上各点对测量基准平面的坐标值，转换为对与评定方法相应的评定基面的坐标值，即需要进行坐标变换。

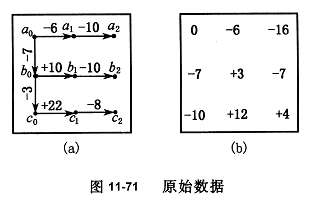
　　[例11—3] 用水平仪按图11—71(a)所示的布线方式测得均布9个点共8个读数，试评定其平面度误差值。
解：
　　按测量方向将各读数顺序累积，并取定起始点a0的坐标值为0，可得图11—71(b)所示各测点的坐标值。

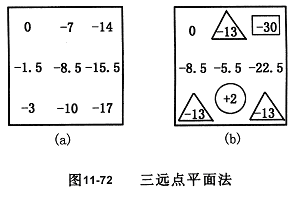
　　用三远点平面法评定时，若选定通过a1、c0、c2三点确定的平面作为评定基面，则经坐标变换后此三点的坐标值应相等，各点的旋转量如图11—72(a)所列，再将图11—71(b)与图11—72(a)对应点的数值相加，即得经坐标变换后的各点坐标值，如图11—72(b)所示，则平面度误差值为：
　　　f=(+2)-(-30)=32 μm

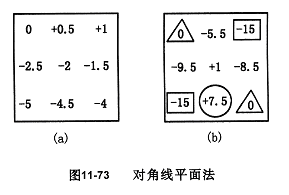
　　用对角线平面法评定时，经坐标变换后应使两对角线上两对角点的坐标值相等，各点的旋转量如图11—73(a)所列，再将图11—71(b)与图11—73(a)对应点的数值相加，即得经坐标变换后的各点坐标值，如图11—73(b)所示，则平面度误差值为：
　　f=(+7.5)-(-15)=22.5 μm